Question

Suppose you can spend no more than 15 hours a week at your two jobs. Moving lawns pays $3 an hour and babysitting pays $5 an hour. You need to earn at least $60 a week.

Answer 1

The system of inequalities are:

`x+y\leq 15\\\\3x+5y\geq 60`

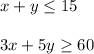
Solution:

Let "x" be the number of hours spent at moving lawn

Let "y" be the number of hours spent at baby sitting

Therefore,

Suppose you can spend no more than 15 hours a week at your two jobs

Which means, you can spend less than or equal to 15 hours

`x+y\leq 15`

Moving lawns pays $3 an hour and babysitting pays $5 an hour. You need to earn at least $60 a week.

Which means, you have to greater than or equal to 60 a week

Therefore,

`3x+5y\geq 60`

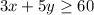
Thus the two inequalities are found