Question

Apple products have become a household name in America with 51% of all households owning at least one Apple product (CNN, March 19, 2012). The likelihood of owning an Apple product is 61% for households with kids and 48% for households without kids. Suppose there are 1,200 households in a representative community, of which 820 are with kids and the rest are without kids.

Let event A correspond to "Household with kids", and B to "Household owns an Apple product".
(a) Are the events "household with kids" and "household without kids" mutually exclusive and exhaustive? Explain.
(b) What is the probability that a household is without kids?
(c) What is the probability that a household is with kids and owns an Apple product?
(d) What is the probability that a household is without kids and does not own an Apple product?

Answer 1

(a) The events of "household with kids" and "household without kids" are mutually exclusive and exhaustive.

(b) The probability that a household is without kids is 0.317.

(c) The probability that a household is with kids and owns an Apple product is 0.417.

(d) The probability that a household is without kids and does not own an Apple product is 0.152.

Explanation:

Denote the events as follows:

X = number of households with kids

A = number of households that own an Apple product.

It is provided that of the 1,200 households in a representative community, 820 are with kids.

The information provided is:

`P(A|X)=0.61\\P(A|X^(c))=0.48\\P(X)=(820)/(1200)=0.683\\`

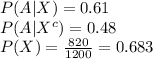
(a)

Mutually exclusive events are those events that cannot occur together.

The event of "household with kids" cannot take place along with the event "household without kids".

Thus, the events of "household with kids" and "household without kids" are mutually exclusive.

Exhaustive events are those events of which at least one will definitely occur.

A household will either have kids or not have kids.

Thus, the events of "household with kids" and "household without kids" are exhaustive.

(b)

Compute the probability that a household is without kids as follows:

`P(X^(c))=1-P(X)=1-0.683=0.317`

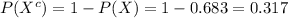
Thus, the probability that a household is without kids is 0.317.

(c)

Compute the probability that a household is with kids and owns an Apple product as follows:

`P(X\cap A)=P(A|X)P(X)=0.61*0.683=0.41663\approx0.417`

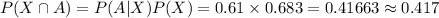
Thus, the probability that a household is with kids and owns an Apple product is 0.417.

(d)

Compute the probability that a household is without kids and does not own an Apple product as follows:

`P(X^(c)\cap A)=P(A|X^(c))P(X^(c))=0.48*0.317=0.15216\approx0.152`

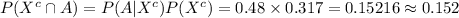
Thus, the probability that a household is without kids and does not own an Apple product is 0.152.