Answer:
The shoe will be 6.251 ft above the ground when it reaches the president.
Explanation:
Let's first find the horizontal and vertical velocity of the shoe.
Horizontal velocity: 24 * Cos(45°) = 16.97 ft/s
Vertical velocity: 24 * Sin(45°) = 16.97 ft/s
Travel time to cover distance between president and reporter:
Travel time = Distance / horizontal velocity
Travel time = 12 / 16.97
Travel time = 0.707 seconds
Now that we know the time we can solve the following motion equation to solve for change in vertical distance after the shoe is thrown:
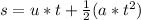
here the initial speed (u) is 16.97 ft/s
the acceleration (a) is -32ft/s^2
and the time is 0.707 seconds
Solving for s we get:
s = 11.998 - 8.747
s = 3.251 ft
Since the shoe was already 3 ft above the ground when we started, we add that to the change in distance:
3 + 3.251 = 6.251 ft
So the shoe will be 6.251 ft above the ground when it reaches the president.