Answer:
a.
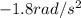
b.

c.52.9 rev
Step-by-step explanation:
We are given that
Initial angular speed of wheel=

Time=t=19 s
Final angular speed=
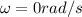
a.We have to find the angular acceleration of the wheel.
We know that
Angular acceleration
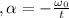
Using the formula
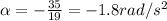
b.
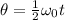
Using the formula
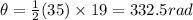
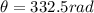
c.
 rad=1 rev
rad=1 rev
1 rad=
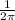 rev
rev
332.5 rad=
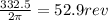
Number of revolutions made by the flywheel in stopping=52.9 rev