Question

Two concentric, hollow spherical shells have radii R1 = 5 cm and R2 = 10 cm. The smaller sphere has a charge of Q distributed uniformly over its surface, while the larger sphere has an opposite charge –Q. Let Q = 7.0 µC. Find the electric field the following distances from the centers of the spheres; give the directions as well, indicating either "away from the center" or "toward the center" (unless the field is zero).a. 2.5 cm from the centersb. 7.5 cm from the centersc. 12.5 cm from the centers

Answer 1

a. E = 0.

b.
`E = 1.29* 10^7~{\rm N/C~away~from~the~center.}`

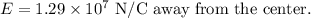
c. E = 0.

Step-by-step explanation:

We will apply Gauss' Law to find the electric field at the given location. We will draw an imaginary spherical shell with radius 'r'. The electric field through the surface of the shell will be equal to the total charge enclosed by this imaginary surface.

Gauss' Law:

`\int\vec{E}d\vec{a} = (Q_(\rm enc))/(\epsilon_0)`

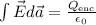
a. r = 2.5 cm (inside the smaller shell)

`E4\pi r^2 = (Q_(enc))/(\epsilon_0) = 0`

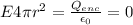
Since there is no charge inside the spheres, the electric field in that region is equal to zero.

b. r = 7.5 cm (between the shells)

`E4\pi r^2 = (Q_1)/(\epsilon_0)\\E = (1)/(4\pi\epsilon_0)(7* 10^(-6))/((7.5* 10^(-2))^2) = 1.29* 10^7~N/C`

Since the charge of the inner surface is positive, the electric field is away from the center.

c. r = 12.5 cm (outside the shells)

Since the total charge of two shells are equal to zero, the electric field outside the shells is zero as well.