Answer:
An Organic Rankine Cycle (ORC) with R-410A has the boiler at 3 MPa superheating to 180°C, and the condenser operates at 800 kPa.
Find all four energy transfers and the cycle efficiency.
The question is solved for steam please plug in the properties for R-410A using the same procedure as below to solve for R-410A
The answers are as follows
(i) At the boiler
Q₁ = 40.73 kJ·kg⁻¹
(ii) At the turbine
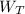 = 2.908 kJ·kg⁻¹
= 2.908 kJ·kg⁻¹
(iii) At the condenser
Q₂ = 40.272 kJ·kg⁻¹
(iv) At the feed pump
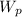 = 2.453 kJ·kg⁻¹
= 2.453 kJ·kg⁻¹
Cycle efficiency is 4.4 %
Step-by-step explanation:
Boiler Pressure p₁ = 3 MPa @ 180 °C
Condenser pressure p₂ = 800 kPa
From the thermodynamics tables we have for steam
At 3 MPa (p₁), 180 °C: h₁ = 764.198 kJ·kg⁻¹
and s₁ = 2.1368 kJ· kg⁻¹· K⁻¹
At 800 kPa (p₂) h₃ =
 = 721.018 kJ·kg⁻¹
= 721.018 kJ·kg⁻¹
s₃ =
 = 2.0460 kJ· kg⁻¹· K⁻¹
= 2.0460 kJ· kg⁻¹· K⁻¹
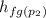 = 2047.28 kJ·kg⁻¹
= 2047.28 kJ·kg⁻¹
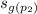 = 6.6615 kJ· kg⁻¹· K⁻¹
= 6.6615 kJ· kg⁻¹· K⁻¹
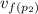 = 0.00111479 m³·kg⁻¹
= 0.00111479 m³·kg⁻¹
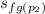 = 4.6156 kJ· kg⁻¹· K⁻¹
= 4.6156 kJ· kg⁻¹· K⁻¹
Since s₁ = s₂
2.1368 =
 + x₂·
+ x₂·
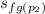 = 2.0460 + x₂·4.6156
= 2.0460 + x₂·4.6156
From where x₂
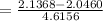 = 0.01967
= 0.01967
Therefore h₂=
 + x₂·
+ x₂·
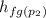 = 721.018+0.01967×2047.28 = 761.29 kJ·kg⁻¹
= 721.018+0.01967×2047.28 = 761.29 kJ·kg⁻¹
h₂ = 761.29 kJ·kg⁻¹

= 0.00111479 m³·kg⁻¹×(3000-800) = 2.453 kJ·kg⁻¹
and
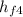 = 2.453 + 721.018 = 723.471 kJ·kg⁻¹
= 2.453 + 721.018 = 723.471 kJ·kg⁻¹
Therefore for 1 kg of fluid we have
Through the implementation of of the steady flow energy equation to the
i) Boiler
ii) Turbine
iii) Condenser
iv) Pump
(i) For the boiler, we have
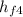 + Q₁ = h₁
+ Q₁ = h₁
Q₁ = h₁ -
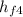 = 764.198 -723.471 = 40.73 kJ·kg⁻¹
= 764.198 -723.471 = 40.73 kJ·kg⁻¹
(ii) For turbine
h₁ =
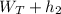 Where
Where
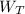 = Work done by turbine
= Work done by turbine
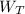 = h₁ -h₂ = 764.198 - 761.29 = 2.908 kJ·kg⁻¹
= h₁ -h₂ = 764.198 - 761.29 = 2.908 kJ·kg⁻¹
(iii) For the condenser we have
h₂ = Q₂ +
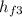 where
where
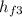 =
=
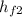 = 721.018 kJ·kg⁻¹
= 721.018 kJ·kg⁻¹
Q₂ = h₂ -
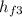 = 761.29 - 721.018 = 40.272 kJ·kg⁻¹
= 761.29 - 721.018 = 40.272 kJ·kg⁻¹
(iv) The feed pump gives
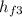 +
+
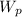 =
=
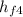 Where,
Where,
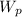 = Work done by pump
= Work done by pump
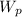 =
=
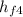 -
-
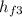 = 723.471 - 721.018 = 2.453 kJ·kg⁻¹
= 723.471 - 721.018 = 2.453 kJ·kg⁻¹
Cycle efficiency is given by
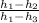 =
=
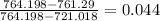 4.4 %
4.4 %
Efficiency of the Rankine cycle is =
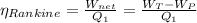
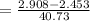 = 0.0112 or 1.12 %
= 0.0112 or 1.12 %