Answer:
a) 0.751 A
b) From the derivation below, it is glaring that the current (I) is independent of θ
Step-by-step explanation:
Given data :
mass of the sphere (m) = 72.0 g = 0.072 kg
number of turns of the wire (N) = 5
radius of the sphere (r) = 19.0 cm = 0.19 m
uniform magnetic field (B) = 0.315
From the given question, the sphere is in translational equilibrium; therefore
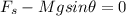
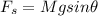 ----------Equation (1)
----------Equation (1)
At the center of the sphere, Lets look at the consideration of the torque; two things is happening;
1) the magnetic field produces a clockwise torque of magnitude μBsinθ
2) the frictional force produces a counterclockwise torque of magnitude
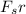
∴
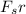 - μBsinθ = 0 ---------- Equation (2)
- μBsinθ = 0 ---------- Equation (2)
Substituting
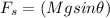 from equation (1) to equation (2); we have:
from equation (1) to equation (2); we have:
mgsinθr - μBsinθ = 0
Dividing both sides by sinθ; we have:
mgr - μB = 0
mgr = μB
μB = mgr ------------------- Equation (3)
Given that:
μ = NIπr²
Substituting μ = NIπr² into Equation (3); we have:
NIπr²B = mgr
Dividing both sides by r; we have:
NIπrB = mg
Making (I) =
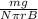
Substituting our given data into equation above; we have:
(I) =
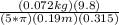
(I) = 0.751 A in counterclockwise direction.
b)
Show that the result does not depend on the value of θ.
From equation (2); we have:
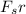 - μBsinθ = 0
- μBsinθ = 0
We also know that;
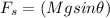 ;
;
so replacing
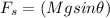 into above equation (2); we have:
into above equation (2); we have:
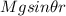 - μBsinθ = 0
- μBsinθ = 0
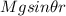 = μBsinθ
= μBsinθ
Dividing both sides by sinθ; we have:
Mgr = μB
However; μ = NIπr²
Substituting it into the above derivation; we have:
Mgr = NIπr²B
Dividing both sides by r; we have:
Mg = NIπrB
Making (I) the subject of the formula; we have:
I =
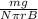
∴ we can conclude that the current is independent on the value of θ.