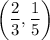Question

Which ordered pair is a solution to the system of linear equations One-half x minus three-fourths y = StartFraction 11 Over 60 EndFraction and Two-fifths x + one-sixth y = StartFraction 3 Over 10 EndFraction? (one-fifth, negative two-thirds) (one-fifth, two-thirds) (two-thirds, negative one-fifth) (two-thirds, one-fifth)

Answer 1

c

Explanation:

2/3, 1/5

Answer 2

`\left((2)/(3),(1)/(5)\right)`

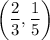
Explanation:

Given the system of two equations:

`\left\{\begin{array}{l}(1)/(2)x-(3)/(4)y=(11)/(60)\\ \\(2)/(5)x+(1)/(6)y=(3)/(10)\end{array}\right.`

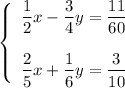
Multiply the first equation and the second equation by 60 to get rid of fractions:

`\left\{\begin{array}{l}30x-45y=11\\ \\24x+10y=18\end{array}\right.`

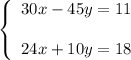
Now multiply the first equation by 4 and the second equation by 5:

`\left\{\begin{array}{l}120x-180y=44\\ \\120x+50y=90\end{array}\right.`

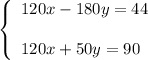
Subtract them:

`(120x-180y)-(120x+50y)=44-90\\ \\120x-180y-120x-50y=-46\\ \\-230y=-46\\ \\y=(46)/(230)=(1)/(5)`

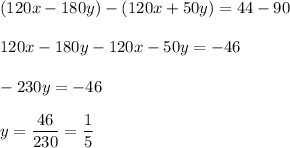
Substitute it into the first equation:

`30x-45\cdot (1)/(5)=11\\ \\30x-9=11\\ \\30x=11+9\\ \\30x=20\\ \\x=(2)/(3)`

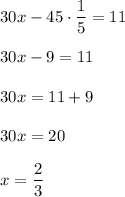
The solution is
`\left((2)/(3),(1)/(5)\right)`