Answer:
(a) 95% confidence interval for the true mean order size = [ 11972.22 , 37067.80 ]
Explanation:
We are given a random sample of 10 shipments of stick-on labels with following order sizes;
12,000, 18,000, 30,000, 60,000, 14,000, 10,500, 52,000, 14,000, 15,700, 19,000
Firstly, Sample mean,
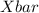 =
=
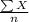
=
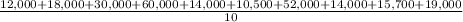 = 24520
= 24520
Sample standard deviation, s =
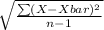 = 17541.81
= 17541.81
The pivotal quantity for confidence interval is given by;
P.Q. =
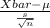 ~
~

So, the 95% confidence interval for true mean order size is given by;
P(-2.262 <
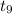 < 2.262) = 0.95
< 2.262) = 0.95
P(-2.262 <
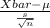 < 2.262) = 0.95
< 2.262) = 0.95
P(-2.262 *
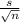 <
<
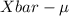 < 2.262 *
< 2.262 *
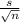 ) = 0.95
) = 0.95
P(Xbar - 2.262 *
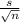 <
<
 < Xbar + 2.262 *
< Xbar + 2.262 *
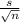 ) = 0.95
) = 0.95
95% confidence interval for
 = [ Xbar - 2.262 *
= [ Xbar - 2.262 *
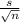 , Xbar + 2.262 *
, Xbar + 2.262 *
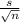 ]
]
= [ 24520 - 2.262*
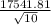 , 24520 - 2.262*
, 24520 - 2.262*
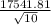 ]
]
= [ 11972.22 , 37067.80 ]