Answer:
At 5% level of significance there is enough evidence to concluded that the residents of Wilmington, Delaware, have more income than the national average.
Explanation:
The national average income of United states is, $44,500.
The hypothesis to test whether the residents of Wilmington, Delaware, have more income than the national average, can be defined as:
H₀: The residents of Wilmington, Delaware, does not have more income than the national average, i.e. μ < $44,500.
Hₐ: The residents of Wilmington, Delaware, have more income than the national average, i.e. μ > $44,500.
It is provided that the distribution of incomes follows a normal distribution.
Given:
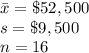
The significance level of the test is, α = 0.05.
As the sample size is small and the population standard deviation is not provided, use the t-test for single mean.
The test statistic is:
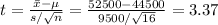
Decision Rule:
If the p value of the test is less than the significance level then the null hypothesis is rejected.
Compute the p value as follows:
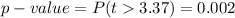
Use the t-table for probability.
The p-value = 0.002 < α = 0.05.
The null hypothesis will be rejected at 5% significance level.
Conclusion:
As the null hypothesis is rejected it implies that the residents of Wilmington, Delaware, have more income than the national average.