Question

Suppose the actual proportion of USU students who feel parking is a problem is 0.70. A student takes a poll of 100 randomly selected Purdue students and asks them if they feel that parking is a problem.

a. What is the mean for the sample proportion?

b. What is the standard deviation for the sample proportion? (Use 4 decimals)

c. What is the probability that the sample proportion is greater than 0.75? (Use 4 decimals)

d. Between what two values does the middle 95% of the sample proportions lie? (Use 4 decimals)

Answer 1

(a) The mean for the sample proportion is 0.70.

(b) The standard deviation for the sample proportion is 0.046.

(c) The probability that the sample proportion is greater than 0.75 is 0.1379.

(d) The two values between which the middle 95% of the sample proportions lie are 0.6080 and 0.7920.

Explanation:

Let X = number of students who feel parking is a problem.

The probability of students who feel parking is a problem is, P (X) = p = 0.70.

The sample of students selected for the poll is, n = 100.

The random variable X follows a Binomial distribution with parameters n = 100 and p = 0.70.

A Normal distribution can be used to approximate the Binomial distribution if np ≥ 10 and n(1 - p) ≥ 10.

Check the condition:

`np=100*0.70=70\\n(1-p)=100*(1-0.70)=30`

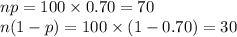
Thus, the distribution of sample proportion (
`\hat p`) is Normal.

(a)

The mean of the sampling distribution of sample proportion is:

`\mu_(\hat p)=\hat p=0.70`

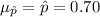
Thus, the mean for the sample proportion is 0.70.

(b)

The standard deviation of the sampling distribution of sample proportion is:

`\sigma_(\hat p)=\sqrt{(\hat p(1-\hat p))/(n)}=\sqrt{(0.70(1-0.70))/(100) } =0.046`

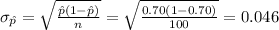
Thus, the standard deviation for the sample proportion is 0.046.

(c)

Compute the probability that the sample proportion is greater than 0.75 as follows:

`P(\hat p>0.7)=P((\hat p-\mu_(\hat p))/(\sigma_(\hat p))>(0.75-0.70)/(0.046) )\\=P(Z>1.09)\\=1-P(Z<1.09)\\=1-0.86214\\=0.13786\\\approx0.1379`

*Use the standard normal table for the probability.

Thus, the probability that the sample proportion is greater than 0.75 is 0.1379.

(d)

It is provided that:

`P(p_(1)<\hat p<p_(2))=0.95`

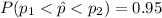
As the sampling distribution of
`\hat p` is Normal then according to the Empirical rule 95% of the data in a Normal distribution falls within 2 standard deviation of mean. That is,

`P(\mu_(\hat p)-2\sigma_(\hat p)<\hat p<\mu_(\hat p)+2\sigma_(\hat p))=0.95`

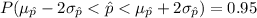
Compute the value of p₁ and p₂ as follows:

`p_(1)=\mu_(\hat p)-2\sigma_(\hat p)=0.70-(2*0.046)=0.608`

`p_(2)=\mu_(\hat p)+2\sigma_(\hat p)=0.70+(2*0.046)=0.792`

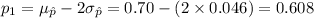
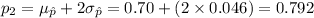
Thus, the two values between which the middle 95% of the sample proportions lie are 0.6080 and 0.7920.