Answer:
a)
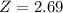
b)
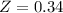
c) The woman, because she has the higher z-score, that is, her height is more standard deviations above the mean.
Explanation:
The z-score, which measures how many standard deviations a score X is above or below the mean, is given by the following formula.

In which
 is the mean and
is the mean and
 is the standard deviation.
is the standard deviation.
(a) What is the z-score for a woman who is 6 feet tall?
The heights of women aged 20 to 29 are approximately Normal with mean 65 inches and standard deviation 2.6 inches. This means that

The mean and the standard deviation are in inches, so X is also must be in inches. Each feet has 12 inches. So X = 6*12 = 72 inches.

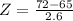
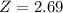
(b) What is the z-score for a man who is 6 feet tall?
Men the same age have mean height 71 inches with standard deviation 2.9 inches. This means that
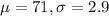
The mean and the standard deviation are in inches, so X is also must be in inches. Each feet has 12 inches. So X = 6*12 = 72 inches.

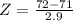
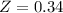
(c) Who is relatively taller?
The woman, because she has the higher z-score, that is, her height is more standard deviations above the mean.