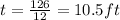Question

A mailbox that is 36 inches tall is beside a tree.The length of the mailboxes shadow is 28 inches.The length of the trees shadow is 98 inches.How tall is the tree in feet.

Answer 1

10.5 feet

Explanation:

In this problem, we have two similar triangles:

- One consists of the mailbox, its shadow and the hypothenuse

- The other one consists of the tree, its shadow and the hypothenuse

The two triangles are similar, so they have same proportions between their sides: therefore, we can apply the rule of three:

`(m)/(s_m)=(t)/(s_t)`

where

m = 36 in is the height of the mailbox

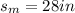`s_m=28 in` is the shadow of the mailbox

t is the height of the tree

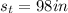`s_t=98 in` is the length of the shadow of the tree

Solving for t, we find the height of the tree:

`t=(m\cdot s_t)/(s_m)=((36)(98))/(28)=126 in`

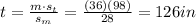
And since

1 feet = 12 inches

The height of the tree in feet is

`t=(126)/(12)=10.5 ft`