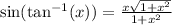Question

Give the exact value of the expression without using a calculator.

sine left parenthesis 2 tangent Superscript negative 1 Baseline eight fifteenths right parenthesis

Answer 1

`\sin \left(\tan^(-1) \left((8)/(15)\right)\right)=(8)/(17)`.

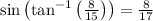Explanation:

To find the exact value of the expression
`\sin(\tan^(-1)((8)/(15) ))`

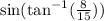
First, we need to simplify the expression
`\sin(\tan^(-1)(x))`.

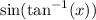Draw a triangle in the plane with vertices
`(1,x)`,
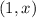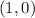`(1,0)`, and the origin. Then
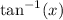`\tan^(-1)(x)` is the angle between the positive x-axis and the ray beginning at the origin and passing through
`(1,x)`.

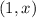Therefore,

`\sin(\tan^(-1)(x))=\frac{x}{\sqrt{1+x^(2) } }`

`\mathrm{Multiply\:by\:the\:conjugate}\:(√(1+x^2))/(√(1+x^2))`

`(x√(1+x^2))/(√(1+x^2)√(1+x^2))`

`√(1+x^2)√(1+x^2)=1+x^2`

`\sin(\tan^(-1)(x))=(x√(1+x^2))/(1+x^2)`

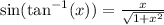
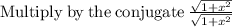
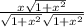
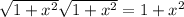
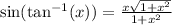
Now, use the identity
`\sin(\tan^(-1)(x))=(x√(1+x^2))/(1+x^2)`

`\sin(\tan^(-1)((8)/(15) ))=\frac{\left((8)/(15)\right)\sqrt{1+\left((8)/(15)\right)^2}}{1+\left((8)/(15)\right)^2}\\\\\frac{(8)/(15)\sqrt{\left((8)/(15)\right)^2+1}}{1+(8^2)/(15^2)}\\\\((136)/(225))/(1+(8^2)/(15^2))\\\\((136)/(225))/(1+(64)/(225))\\\\(136)/(225\cdot (289)/(225))\\\\(136)/(289)=(8)/(17)\\\\\sin \left(\tan^(-1) \left((8)/(15)\right)\right)=(8)/(17)`