Question

The television show CSI: Shoboygan has been successful for many years. That show recently had a share of 18, meaning that among the TV sets in use, 18% were tuned to CSI: Shoboygan. Assume that an advertiser wants to verify that 18% share value by conducting its own survey, and a pilot survey begins with 14 households have TV sets in use at the time of a CSI: Shoboygan broadcast. Find the probability that none of the households are tuned to CSI: Shoboygan. P(none) = Find the probability that at least one household is tuned to CSI: Shoboygan. P(at least one) = Find the probability that at most one household is tuned to CSI: Shoboygan. P(at most one) = If at most one household is tuned to CSI: Shoboygan, does it appear that the 18% share value is wrong? (Hint: Is the occurrence of at most one household tuned to CSI: Shoboygan unusual?)

Answer 1

(a) The value of P (None) is 0.062.

(b) The value of P(at least one) is 0.938.

(c) The value of P(at most one) is 0.253.

(d) The event is not unusual.

Explanation:

Let X = number of households watching the show.

The probability of the random variable x is, P (X) = p = 0.18.

The sample selected for the survey is of size, n = 14

The random variable X follows a Binomial distribution with parameter n = 14 and p = 0.18.

The probability of a Binomial distribution is computed using the formula:

`P(X=x)={n\choose x}p^(x)(1-p)^(n-x);\ x=0,1,2,...`

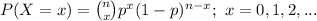
(a)

Compute the probability that none of the households are tuned to CSI: Shoboygan as follows:

`P(X=0)={14\choose 0}(0.18)^(0)(1-0.18)^(14-0)=1*1*0.06214=0.062`

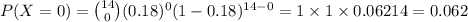
Thus, the value of P (None) is 0.062.

(b)

Compute the probability that at least one household is tuned to CSI: Shoboygan as follows:

P (X ≥ 1) = 1 - P (X < 1)

= 1 - P (X = 0)

`=1-0.062\\=0.938`

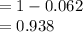
Thus, the value of P(at least one) is 0.938.

(c)

Compute the probability that at most one household is tuned to CSI: Shoboygan as follows:

P (X ≤ 1) = P (X = 0) + P (X = 1)

`={14\choose 0}(0.18)^(0)(1-0.18)^(14-0)+{14\choose 1}(0.18)^(1)(1-0.18)^(14-1)\\=0.062+0.191\\=0.253`

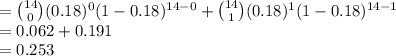
Thus, the value of P(at most one) is 0.253.

(d)

An event that has a very low probability of occurrence is known as an unusual event.

The probability of the event "at most one household is tuned to CSI: Shoboygan" is 0.253.

This probability value is not low.

Hence, the event is not unusual.