Question

On a can of sardines it is written that the can contains 10 sardines. You open up 100 cans and find the average is 9.75 sardines with a standard deviation of 1.

What is the test statistic in a test of the null hypothesis that the population average is 10?

Answer 1

Answer:
`t= -2.5`

Explanation:

By considering the given statements :

Null hypothesis :
`\mu=10`

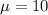
Alternative hypothesis :
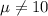`\mu\\eq10` ( opposite of null hypothesis.)

As per given , we have

Sample size : n= 100

Sample mean :
`\overline{x}=9.75`

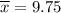
Sample standard deviations :
`s=1`

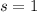
Since population standard deviation is unknown , so we will perform t-test.

Formula for test statistic ( for population mean):

`t=\frac{\overline{x}-\mu}{(s)/(√(n))}\\\\=(9.75-10)/((1)/(√(100)))\\\\=(-0.25)/((1)/(10))=-0.25*10=-2.5`

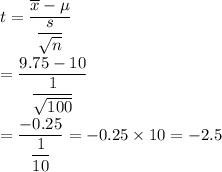
Hence, the required test statistic :
`t= -2.5`