Question

Find the range of the function f(x)=10-x squared

Answer 1

I'll assume x is squared, case in which the function looks like this:

`f(x) = 10-x^(2)`

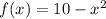
The range is (-∞; 10] and be careful at those parentheses

Explanation:

You could, for example, think of what happens to x for different situations.

If x is very big,
`x^(2)` is even bigger. 10 -
`x^(2)` thus gets smaller, because you're subtracting something bigger and bigger. So, it tends to negative infinity.

Now, if x is any bigger than 10, it'll be a negative result, so

x>10 ==> f(x)<0

actually, this happens for any x>
`√(10)`

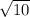
For x negative, smaller (more negative) than -
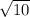`√(10)`, the result is the same.

If x is in the range
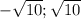`-√(10); √(10)` then the result becomes positive, since we're subtracting something smaller than 10. The biggest result we could ever achieve is when x=0. Thus 10 - 0 = 10.

In conclusion, 10 is the "upper limit" and -∞ is the "lower limit".

Thus, the range is (-∞ ; 10] AND BE CAREFUL AT PARENTHESES.