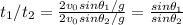Question

The battleship and enemy ships 1 and 2 lie along a straight line. Neglect air friction. battleship 1 2 Consider the motion of the two projectiles fired at t = 0. Their initial speeds are both v0 but they are fired with different initial angles θ1 and θ2 with respect to the horizontal. What is the ratio of the times of the flights?

Answer 1

`(t_1)/(t_2) = (sin\theta_1)/(sin\theta_2)`

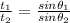
Step-by-step explanation:

The vertical component of the initial velocities are

`v_v = v_0sin\theta`

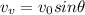
If we ignore air resistance, and let g = -9.81 m/s2. The the time it takes for the projectiles to travel, vertically speaking, can be calculated in the following motion equation

`v_vt - gt^2/2 = s = 0`

`t(v_v - gt/2) = 0`

`v_v - gt/2 = 0`

`t = 2v_v/g = 2v_0sin\theta/g`

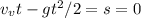
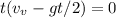
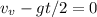
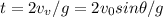
So the ratio of the times of the flights is

`t_1 / t_2 = (2v_0sin\theta_1/g)/(2v_0sin\theta_2/g) = (sin\theta_1)/(sin\theta_2)`