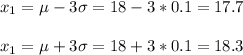Answer:
1. z_bolt = 1.2
z_nut=-2.1
2. A bolt with a diameter of 18.08 mm is less than one SD of the mean.
3. It is more likely a bolt larger than 18.12 mm.
4. The bolt larger than 18.23 mm is more likely.
5. About 50% of nuts are smaller than 18 mm
6. About 95% of bolts are approximately between 17.804 mm and 18.196 mm
7. About 99.7 % of nuts are approximatelly between 17.7 mm and 18.3 mm
Explanation:
Bolts: Mean: 18.00 mm SD: 0.10 mm
Holes: Mean: 18.70 mm SD:0.08 mm
1. Find the z-score for a Bolt of 18.12mm Nut of 18.532mm
Bolt
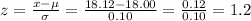
Hole
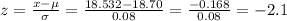
2. How many standard deviations away from the average is a bolt with a diameter of 18.08mm?
Because the SD is 0.1 mm, we can say that a bolt with a diameter of 18.08 mm is less than one SD of the mean (<18.10 mm).
3. Which is more likely Bolt smaller than 17.84mm Bolt larger than 18.12mm
We have to calculate the probability of both.
Bolt #1
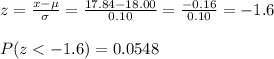
Bolt #2
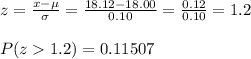
It is more likely a bolt larger than 18.12 mm.
4. Which is more likely Bolt larger than 18.23mm Nut smaller than 18.548mm
Bolt
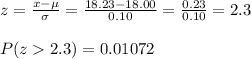
Nut
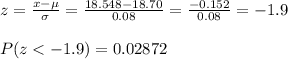
The bolt larger than 18.23 mm is more likely.
5. About 50% of nuts are smaller than 18 mm
6. About 95% of bolts are approximately between 17.804 mm and 18.196 mm
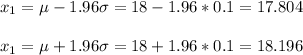
7. About 99.7 % of nuts are approximatelly between 17.7 mm and 18.3 mm