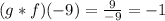Question

If f(x)=3/x and g(x)=3x, which of the following statements is true?

a. (f*g)(2)=2
b. (g*f)(2)=0
c.(f*g)(9)=1
d. (g*f)(-9)=-1

Answer 1

d. (g*f)(-9)=-1

Explanation:

In this problem, we have two functions:

`f(x)=(3)/(x)`

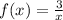
and

`g(x)=3x`

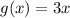
The notation:

(f*g)(x) represents the composite function of f and g; this can be calculated by using the output of g(x) as input for f(x), in other words:

`(f*g)(x)=f(g(x))`

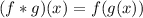
Simiarly, the notation (g*f)(x) can be calculated by using the output of f(x) as input for g(x), mathematically:

`(g*f)(x)=g(f(x))`

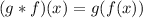
Using the definitions of f(x) and g(x), we can derive an expression for the two composite functions here:

`(f*g)(x)=f(g(x))=(3)/(g(x))=(3)/(3x)=(1)/(x)`

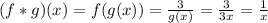
And

`(g*f)(x)=3(f(x))=3((3)/(x))=(9)/(x)`

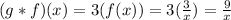
Now we can analyze the given statements:

a. (f*g)(2)=2 --> FALSE, because
`(f*g)(2)=(1)/(2)`

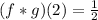
b. (g*f)(2)=0 --> FALSE, because
`(g*f)(0)=(9)/(0)=\infty`

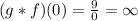
c.(f*g)(9)=1 --> FALSE, because
`(f*g)(9)=(1)/(9)`

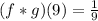
d. (g*f)(-9)=-1 --> TRUE, because
`(g*f)(-9)=(9)/(-9)=-1`