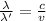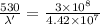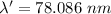Question

In a physics lab, light with a wavelength of 530 nm travels in air from a laser to a photocell in a time of 16.7 ns . When a slab of glass with a thickness of 0.870 m is placed in the light beam, with the beam incident along the normal to the parallel faces of the slab, it takes the light a time of 21.3 ns to travel from the laser to the photocell.

What is the wavelength of the light in the glass?

Use 3.00×108 m/s for the speed of light in a vacuum. Express your answer using two significant figures.

Answer 1

`\lambda'=78.086\ nm`

Step-by-step explanation:

Given:

• wavelength of light in the air,
  `\lambda=530* 10^(-9)\ m`

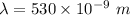
• time taken to travel from the source to the photocell via air,
  `t=16.7\ s`

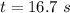
• time taken to reach the photocell via air and glass slab,
  `t'=21.3* 10^(-9)\ s`

• thickness of the glass slab,
  `x=0.87\ m`

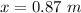
Now we have the relation for time:

`\rm time=(distance)/(speed)`

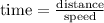
hence,

`t=(d)/(c)`

c= speed of light in air

`16.7* 10^(-9)=(d)/(3* 10^8)`

`d=16.7* 10^(-9)* 3* 10^8`

`d=5.01\ m`

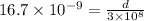
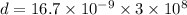
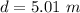
For the case when glass slab is inserted between the path of light:

`((d-x))/(c) +(x)/(v) =t'` (since light travel with the speed c only in the air)

here:

v = speed of light in the glass

`((5.01-0.87))/(3* 10^8) +(0.87)/(v) =21.3* 10^(-9)`

`v=4.42* 10^7\ m.s^(-1)`

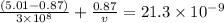
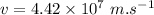
Using Snell's law:

`(\lambda)/(\lambda') =(c)/(v)`

`(530)/(\lambda') =(3* 10^8)/(4.42* 10^7)`

`\lambda'=78.086\ nm`