Question

Pls help 100 points will mark correct answer

Which of the following describes a linear function?

A. It is V shaped and passes through the origin.
B. It is a straight line in one portion and a curve in another portion.
C. Its y-values decrease at a constant rate as its x-value increases.
D. Its y-values increase at a nonconstant rate as its x-value increases.

Answer 1

C. Its y-values decrease at a constant rate as its x-value increases.

Explanation:

A linear function is described by the following relationship:

`y=mx+q`

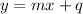
where

x, y are the two variables

m is the slope of the function

q is the y-intercept of the function

The y-intercept represents the value of y at which x = 0, so it just corresponds to a "rigid shift" of the function along the y-axis.

Therefore for the purpose of this problem we can consider a linear function passing through the origin (0,0):

`y=mx`

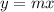
m (the slope) represents the rate of change of the function. For a linear function, m is constant: this means that

- if m is positive, as x increases, then y increases at a constant rate

- if m is negative, as x increases, then y decreases at a constant rate

Therefore, the correct option describing a linear function is

C. Its y-values decrease at a constant rate as its x-value increases.