Answer:
2.5 times more intense.
Explanation:
For the 6.2 magnitude earthquake, the Richter model gives us
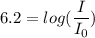
where
 is the intensity of the 6.2 earthquake.
is the intensity of the 6.2 earthquake.
And for the 5.8 magnitude earthquake,
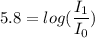
where
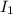 is the intensity of the 5.8 earthquake.
is the intensity of the 5.8 earthquake.
Now, we subtract the two equations to get:
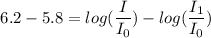
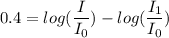
Now using the logarithmic property
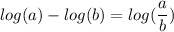
our equation becomes
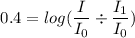
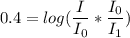
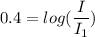
take both sides to the 10th power and get:


Therefore, the earthquake was 2.5 times more intense.