Answer:
A) The graph of f(x) = x2 is made narrower.
Explanation:
The transformed graph has equation:

To see the transformations clearly, we need to rewrite the function in the vertex form:
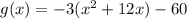
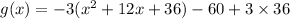
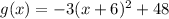
Therefore, the graph of the original function is made narrow of the multplier, 3.
The correct answer is A