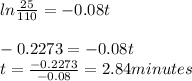Answer:
(b)185
(c)7.03 minutes and 2.84 minues
Explanation:
(a) In the function
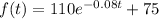 , the exponential function has a negative power and
, the exponential function has a negative power and
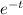 decreases for increasing value of t and tends to zero as t tends to infinity
decreases for increasing value of t and tends to zero as t tends to infinity
(b)At the beginning of the experiment, t=0
Therefore
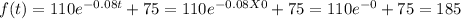
(c)If the temperature f(t)=140 degrees
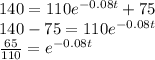
Taking the natural logarithm of both sides
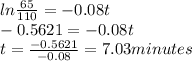
If the temperature f(t)=100 degrees
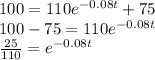
Taking the natural logarithm of both sides