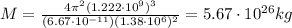Question

itan's orbital radius is about 1222000 km and its orbital period is just under 16 days. From this information, estimate the mass of Saturn (in kg) to 2 sig figs. Use "e-notation" to report your answer.

Answer 1

`5.67\cdot 10^(26) kg`

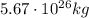
Step-by-step explanation:

For a satellite in orbit around a planet, the gravitational force between the planet and the satellite is equal to the centripetal force that keeps the satellite in circular motion.

So, we can write:

`(GMm)/(r^2)=m(v^2)/(r)`

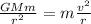
where

G is the gravitational constant

M is the mass of the planet

m is the mass of the satellite

r is the orbital radius of the satellite

v is the speed of the satellite

The equation can be rewritten as

`M=(v^2r)/(G)`

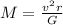
Also, we can write the orbital speed as the ratio between the length of the orbit (circumference of the orbit) and orbital period, T:

`v=(2\pi r)/(T)`

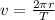
Substituting into the equation for M,

`M=(4\pi^2 r^3)/(GT^2)`

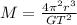
Here we have:

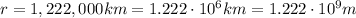`r=1,222,000 km = 1.222\cdot 10^6 km = 1.222\cdot 10^9 m` is the orbital radius

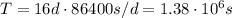`T=16 d \cdot 86400 s/d=1.38\cdot 10^6 s` is the orbital period

Substituting, we find the mass of the Saturn:

`M=(4\pi^2 (1.222\cdot 10^9)^3)/((6.67\cdot 10^(-11))(1.38\cdot 10^6)^2)=5.67\cdot 10^(26) kg`