Answer:
The population alternates between increasing and decreasing
Explanation:
The options of the question are
A) The population density decreases each year.
B) The population density increases each year.
C) The population density remains constant.
D) The population alternates between increasing and decreasing
we have
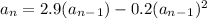
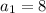
Find the value of
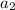
For n=2
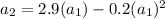
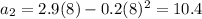
Find the value of
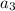
For n=3
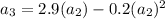
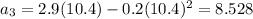
For n=4
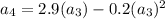
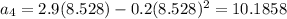
For n=5
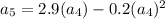

therefore
The population alternates between increasing and decreasing