Question

What is the true solution to the logarithmic equation below? log Subscript 4 Baseline left-bracket log Subscript 4 Baseline (2 x) right-bracket = 1

x = 2
x = 8
x = 64
x = 128

Answer 1

Explanation:

`log_4(log_4 2x)=1 \\ \\ \therefore \: log_4 2x = {4}^(1) \\ \\ \therefore \: log_4 2x =4 \\ \\ \therefore \: 2x = {4}^(4) \\ \\ \therefore \: 2x = 256 \\ \\ \therefore \: x = (256)/(2) \\ \\ \therefore \: x = 128`

Answer 2

x = 128

Explanation:

The given logarithm is

`log_(4)(log_(4)(2x))=1`

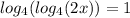
To find the value of
`x`, we need to uses some logarithm and exponent properties.

First, we have

`log_(a)M=b \implies a^(b)=M`

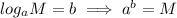
Applying this property, we have

`log_(4)(log_(4)(2x))=1\\4^(1)= log_(4)(2x)`

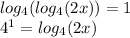
Then, we use the property again

`4^(4)=2x`

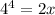
Now, we solve for
`x`

`x=(256)/(2)\\ x=128`

Therefore, the right answer is the last choice: x = 128.