Question

When one person shouts at a football game, the sound intensity level at the center of the field is 63.0 dB. When all the people shout together, the intensity level increases to 113 dB. Assuming that each person generates the same sound intensity at the center of the field, how many people are at the game?

Answer 1

There were approximately 148 people at the game.

Explanation:

The decibal is represented as:

`dB = 10\log((l)/(l_0))`

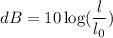
We are given that:

One person creates a intensity of 63.0 dB

Thus, we can write:

`63 = 10\log((l_1)/(l_0))`

Let x number of people give an intensity of 113 dB, thus, we can write:

`113 = 10\log((xl_1)/(l_0))\\\\113 = 10\bigg(\log((l_1)/(l_0))+\log x \bigg)\\\\113 = \bigg(10\log((l_1)/(l_0))+10\log x \bigg)\\\\113 = 63+10\log x\\50 = 10\log x\\\log x = 5\\x = e^5=148.4131`

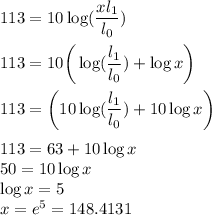
Thus, there were approximately 148 people at the game.