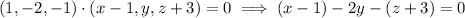Question

20. Find an equation for the plane parallel to 3x − 3y + 2x = 5 and through the point (4, 3, 5). 21. Find an equation for the plane orthogonal to the line x(t) = (2 + t, 3 − 2t, 1 − t) and through (1, 0, −3).

Answer 1

20. I suppose you meant to write
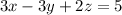`3x-3y+2z=5`? This plane has normal vector (3, -3, 2), so the equation of the plane parallel to this one that goes through (4, 3, 5) is

`(3,-3,2)\cdot(x-4,y-3,z-5)=0\implies3(x-4)-3(y-3)+2(z-5)=0`

`\implies 3x-3y+2z=13`

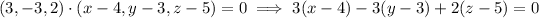
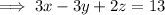
21. The tangent to
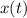`x(t)` is parallel to the normal vector to the plane, so we can simply use it as the normal vector. This tangent vector is

`(\mathrm dx(t))/(\mathrm dt)=(1,-2,-1)`

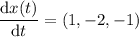
Then the plane has equation

`(1,-2,-1)\cdot(x-1,y,z+3)=0\implies(x-1)-2y-(z+3)=0`

`\implies x-2y-z=4`