Question

Refer to the Current Allergy & Clinical Immunology (March 2004) study of latex allergy in health care workers. There is a claim that the mean number of latex gloves used per day by all hospital employees is less than 20 gloves. A sample of 46 were selected with a mean number of latex gloves used per day by all hospital employees of 19.3 and standard deviation of 11.9. Assume alpha is 0.01. (b) What is the test statistic?

Answer 1

Explanation:

Hello!

The researcher wants to test if the average number of latex gloves used per day by all hospital employees is less than 20, symbolically: μ < 20

A sample of 46 workers was selected and a sample means of X[bar]= 19.3 and a sample standard deviation of S= 11.9.

The study variable is X: number of latex gloves used per day by a hospital employee.

There is no information about the variable distribution, but since the sample is large enough (n≥30) we can apply the Central Limit Theorem and approximate the distribution of the sample mean to normal X[bar]≈N(μ;δ²/n)

The hypotheses are:

H₀: μ ≥ 20

H₁: μ < 20

α: 0.01

The statistic to use is the standard normal approximation:

`Z= (X[bar]-Mu)/((Sigma)/(√(n) ) )`

`Z_(H_0)= (19.3-20)/((11.9)/(√(46) ) )= -0.398 = -0.4`

With critical level
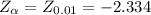`Z_(\alpha ) = Z_(0.01) = -2.334`, considering the test is one-tailed left, the calculated Z value is greater than the critical value so the decision is to not reject the null hypothesis.

I hope it helps!