Question

A team of dogs accelerates a 290kg dogsled from 0 to 6.0m/s in 3.0 s. Assume that the acceleration is constant.

Part A
What is the magnitude of the force exerted by the dogs on the sled?
Part B
What is the work done by the dogs on the sled in the 3.0 s?
Part C
What is the instantaneous power of the dogs at the end of the 3.0 s?
Part D
What is their instantaneous power at 1.5 s?

Answer 1

A) 580 N B) 5,220 J C) 1,740 W D) 870W

Step-by-step explanation:

A)

• Assuming no friction present (or that is negligible) the force exerted by the dogs on the sled must meet Newton's 2nd law:

`F = m*a (1)`

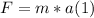
• We can find the value of the acceleration (assumed to be constant), just applying the definition of acceleration, as follows:

`a =\frac{v_{}-v_(0)}{t-t_(0)}`

• where v = 6.0 m/s, v₀=0, t(0)=0, t=3.0s
• Replacing by the values above, and solving for a:

`a =(6.0m/s)/(3.0s) = 2 m/s2`

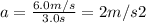
• Replacing this value of a , and m= 290 kg, in (1), we get:

`F = m*a = 290 kg*2 m/s2 = 580 N`

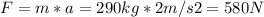
• The magnitude of the force exerted by the dogs on the sled is 580 N.

B)

• In order to be able to find the work done during the 3.0 s, we need to find the displacement produced by the force during that time.
• As the acceleration is assumed to be constant, and the sled starts from rest, we can use the following kinematic equation:

`x = (1)/(2) * a * t^(2)`

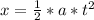
• Replacing by the values of a and t, we can find the displacement x (assuming x₀ = 0), as follows:

`x = (1)/(2) * 2 m/s2 * (3.0s)^(2) = 9 m`

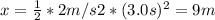
• So, the work done by the force F can be found as follows:
• W = F * d = 580 N* 9 m = 5,220 J
• (An identical outcome could have been found applying the work-energy theorem).

C)

• The instantanous power can be calculated as follows:

`P =(W)/(\Delta t)`

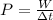
• Replacing W= 5,220 J and t = 3.0 s, we have:

`P = (W)/(\Delta t) = (5220 J)/(3.0s) = 1,740 W`

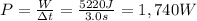
• The instantaneous power, at the end of the 3.0 s, is 1,740 W.

D)

• We can find the instantaneous power at t=1.5 s, using the same equation as above:

`P =(W)/(\Delta t)`

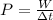
• Now, we need first to know the work done during the first 1.5s.
• We need to find the displacement at the end of the 1.5s time:

`x = (1)/(2) * a * t^(2) = (1)/(2) * 2 m/s2 * (1.5s)^(2) = 2.25 m`

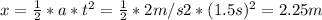
• We can find now the work done at the end of the first 1.5s, as follows:
• W = F * d = 580 N * 2.25 m = 1,305J
• The instantaneous power can be found as follows:

`P = (W)/(\Delta t) = (1,305 J)/(1.5.0s) = 870 W`

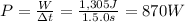
• The instantaneous power, at the end of the first 1.5s, is 870 W.