Answer: 6630
Explanation:
Given , Number of documentaries = 17
Number of children's movies = 20
Total movies = 17+20=37
Number of combinations of r things taken out of things =
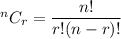
Now, the number of different combinations of 3 movies can she rent if she wants at least one documentary
= (1 documentary+2 children's movies , 2 documentary+1 children's movies , 3 documentary+0 children's movies)
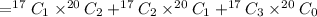
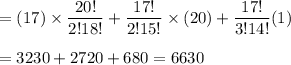
Hence, the number of different combinations of 3 movies can she rent if she wants at least one documentary is 6630 .