Question

If ab passes through the point (2,3) and is perpendicular to y=2x-7, find the equation of ab in general form.

Show full working out ty ;)

Answer 1

2y + x = 8

Explanation:

Since ab is perpendicular to the given line (with m1 = 2)

m1×m2 = -1

m2 = -½

y = -½x + c

When x = 2 , y = 3

3 = -½(2) + c

c = 3+1 = 4

y = -½x + 4

Multiply by 2

2y = -x + 8

2y + x = 8

Answer 2

x + 2y - 8 = 0

Explanation:

The equation of a line in slope- intercept form is

y = mx + c ( m is the slope and c the y- intercept )

y = 2x - 7 ← is in slope- intercept form

with slope m = 2

Given a line with slope m then the slope of a line perpendicular to it is

`m_(perpendicular)` = -
`(1)/(m)` = -
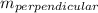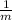`(1)/(2)`, thus

y = -
`(1)/(2)` x + c ← is the partial equation

To find c substitute (2, 3) into the partial equation

3 = - 1 + c ⇒ c = 3 + 1 = 4

y = -
`(1)/(2)` x + 4 ← equation in slope- intercept form

The equation of a line in general form is

Ax + By + C = 0 ( A is a positive integer and B, C are integers )

Multiply the slope- intercept equation through by 2

2y = - x + 8 ( add x to both sides )

x + 2y = 8 ( subtract 8 from both sides )

x + 2y - 8 = 0 ← in general form