Since we assume the outcome of the games are independent and the probability that A wins any one game is p. We will have that:
The probability that:
Team A wins in 5 games =
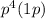
Team B wins in 5 games =
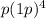
Since there are 4 ways each team can win in 5 games, the probability that the series last 5 games is:
![4[p^(4) (1p)+p(1p)^(4) ]](https://img.qammunity.org/2021/formulas/mathematics/high-school/c9q06guumfpz24u1vhej7d1xgzpgh6tj78.png)
Thus, the answer is:
![4[p^(4) (1p)+p(1p)^(4) ]](https://img.qammunity.org/2021/formulas/mathematics/high-school/c9q06guumfpz24u1vhej7d1xgzpgh6tj78.png)