Question

Assuming that the laptop replacement times have a mean of 3.3 years and a standard deviation of 0.6 years, find the probability that 41 randomly selected laptops will have a mean replacement time of 3.1 years or less.

Answer 1

Required Probability = 0.01659

Explanation:

We are given that the laptop replacement times have a mean of 3.3 years and a standard deviation of 0.6 years i.e.;
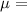`\mu =` 3.3 years and
`\sigma` = 0.6 years

Sample of 41 is taken i.e. n = 41.

The Z score probability is given by;

Z =
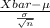`(Xbar -\mu)/((\sigma)/(√(n) ) )` ~ N(0,1)

Let X bar = mean replacement time

So, probability that randomly selected laptop have a mean replacement time of 3.1 years or less = P(X bar <= 3.1 years)

P(X bar <= 3.1) = P(
`(Xbar -\mu)/((\sigma)/(√(n) ) )` <=
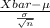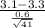`(3.1 -3.3)/((0.6)/(√(41) ) )` ) = P(Z <= -2.13) = 1 - P(Z < 2.13)

= 1 - 0.98341 = 0.01659

Therefore, probability that 41 randomly selected laptops will have a mean replacement time of 3.1 years or less is 0.01659 .