Answer:
Explanation:
Given that at time t, the position of a body moving along the s-axis is sequalsnegative t cubed plus 15 t squared minus 72 t m
i.e.
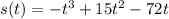
Velocity is nothing but s'(t) = derivative of s
and acceleration is s"(t) = derivative of v(t)
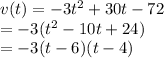
a) v(t) =0 when t = 4 or 6
b)
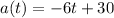
a(t) =0 when t =5
c) Distance travelled by the body from 0 to 5 would be

i.e. 110 miles (distance cannot be negative)