Answer: Correct answer is

Explanation:
Irrational number is one which cannot be written in the form of p/q.The square root of 32 is an irrational number, which means if we convert it into a decimal point, it would continue and will not stop.It means it will be non-terminating and non repeating decimals.The square root of 32 will not end and it's will have non repeating digits also.
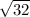 is
is
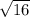 *
*
 .
.
⇒
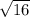 = 4
= 4
⇒ so
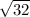 = 4*
= 4*

now square root of 32 comes out to be 4*

we will multiply it with
 to get a rational product
to get a rational product
i.e 4*
 *
*
 (
(
 *
*
 = 2 )
= 2 )
⇒ 4*2
⇒ 8
we obtain 8 as a rational number. so
 is the smallest number with which we will multiply square root of 32 to get a rational product.
is the smallest number with which we will multiply square root of 32 to get a rational product.