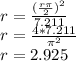Question

At t1 = 1.00 s, the acceleration of a particle moving at constant speed in counterclockwise circular motion is At t2 = 2.00 s (less than one period later), the acceleration is The period is more than 1.00 s. What is the radius of the circle?

Answer 1

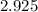`2.925` meters

Step-by-step explanation:

See the remaining part of required information in the attached image

Solution

The formula for calculating velocity is equal to

`v = (r\theta)/(t_2 - t_1)`

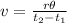
Where v is the velocity,
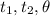`t_1, t_2,\theta` are time range for two acceleration vectors and angle between two acceleration vector respectively and r is the radius of the circle

Putting the give values in above equation we get

`v = (r * (\pi )/(2) )/(2 -1) \\v = (r\pi )/(2)`

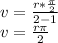
Acceleration is equal to

`√(6^2 + 4^2) \\√(36+16) \\√(52) \\= 7.21`

Radius is equal to

`(v^2)/(a)`

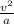
Putting the given values we get -

`r = (((r\pi )/(2))^2)/(7.211) \\r = (4 * 7.211 )/(\pi^2 ) \\r = 2.925`