Question

Suppose that the net resistance comes from two resistors in series: R=R1+R2. Assume that you measure each resistor independently, multiple times in multiple ways, obtaining these mean values and uncertainties: R1={1.234+/-0.007} Ohms and R2={3.142+/-0.014} Ohms. The mean value of the net resistance is (of course): R=4.376 Ohms. Calculate the net uncertainty in this value of R (also in Ohms).

Answer 1

`\Delta R=0.021\ \Omega`

Step-by-step explanation:

Given:

The resistances in series:

• 
  `R_1=1.234\pm 0.007\ \Omega`

• 
  `R_2=3.142\pm0.014\ \Omega`

• Mean value of net resistance,
  `R_m=4.376\ \Omega`

We know that the resultant of the resistances in series is given as:

`R=R_1+R_2`

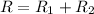
For the maximum possible deviation in the values being added we take the limits only on one side of the mean values for all the parameters.

`R=(1.234+0.007)+(3.142+0.014)\\R=(4.376+0.021)\ \Omega`

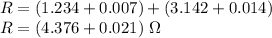
Therefore the net uncertainty in the value:

`\Delta R=0.021\ \Omega`

Answer 2

± (.021 ) ohm

Step-by-step explanation:

In the addition of two physical quantities , the uncertainties are simply added .

So , net uncertainty in the value of R will be

± (.007 +.014)

=± (.021 ) ohm