Answer:
The forces experienced by the two asteroids are the same.
The asteroid with the smaller mass will have the greater acceleration. i.e it has twice the acceleration of the asteroid with the larger mass.
Step-by-step explanation:
Newton's law of gravitation states that the force (
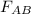 ) exerted by an object of mass A (
) exerted by an object of mass A (
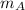 ) on another object of mass B (
) on another object of mass B (
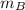 ) is the same as the force (
) is the same as the force (
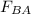 ) exerted by the object of mass B on the object of mass A and also, this force is directly proportional to the product of the two masses and inversely proportional to the square of the distance (r) between these two masses. i.e
) exerted by the object of mass B on the object of mass A and also, this force is directly proportional to the product of the two masses and inversely proportional to the square of the distance (r) between these two masses. i.e
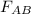 =
=
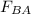 = k
= k
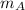
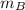 / r² -----------------(i)
/ r² -----------------(i)
Now, to the question,
Let the mass of the first asteroid be
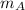 and
and
the mass of the second asteroid be
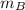 .
.
(a) The individual forces (F) experienced by the two asteroids are the same and will be given by;
F = k
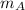
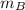 / r²
/ r²
From the question,
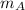 = 2 x
= 2 x
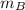
Substitute the value of
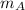 = 2 x
= 2 x
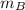 into equation (ii) as follows;
into equation (ii) as follows;
=> F = 2 k
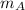
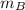 / r²
/ r²
(b) Now, let's find the acceleration of each asteroid using Newton's second law of motion as follows;
F = m x a --------------------(iii)
Where;
F = force on the object
m = mass of the object
a = acceleration of the object
(i) To get the acceleration (
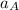 ) of the first asteroid, substitute:
) of the first asteroid, substitute:
m =
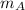 = 2 x
= 2 x
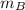 and;
and;
a =
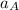
into equation (iii) as follows;
F = 2 x
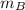 x
x
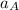
=>
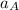 = F / (2 x
= F / (2 x
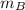 ) ---------------(iv)
) ---------------(iv)
(i) To get the acceleration of the second asteroid (
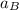 ), substitute
), substitute
m =
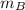 and;
and;
a =
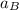
into equation (iii) as follows;
F =
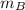 x
x
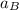
=>
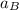 = F /
= F /
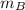 -----------------(v)
-----------------(v)
Since the forces on the two bodies are the same, lets divide equation (iv) by equation(v) as follows;
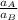 =
=
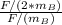
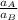 =
=

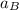 = 2 x
= 2 x
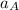
Therefore, the acceleration of the second asteroid is twice that of the first asteroid (the one with twice the mass of the first asteroid).