Question

An electron is released from rest at a distance of 0.570 m from a large insulating sheet of charge that has uniform surface charge density 4.60×10−12 C/m2 . Part A How much work is done on the electron by the electric field of the sheet as the electron moves from its initial position to a point 6.00×10−2 m from the sheet?

Answer 1

The work done is
`2.12*10^(-20)\ J` and 0.1325 eV.

Step-by-step explanation:

Given that,

Distance = 0.570 m

Surface charge density
`\sigma=4.60*10^(-12)\ C/m^(2)`

Using formula of electric field

`E = (\sigma)/(2\epsilon_(0))`

Using formula of electrostatic force ,

`F = eE`

`F=e*((\sigma)/(2\epsilon_(0)))`

(A). We need to calculate the work done

Using formula of work done

`W=Fd`

`W=e*((\sigma)/(2\epsilon_(0)))d`

Put the value into the formula

`W=1.6*10^(-19)*((4.60*10^(-12))/(2*8.85*10^(-12)))*(0.570-6.00*10^(-2))`

`W=2.12*10^(-20)\ J`

`W=(2.12*10^(-20))/(1.6*10^(-19))\ ev`

`W=0.1325\ eV`

Hence, The work done is
`2.12*10^(-20)\ J` and 0.1325 eV.

Answer 2

Step-by-step explanation:

Formula to calculate the electric field of the sheet is as follows.

E =
`(\sigma)/(2 \epsilon_(o))`

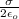
And, expression for magnitude of force exerted on the electron is as follows.

F = Eq

So, work done by the force on electron is as follows.

W = Fs

where, s = distance of electron from its initial position

= (0.570 - 0.06) m

= 0.51 m

First, we will calculate the electric field as follows.

E =
`(\sigma)/(2 \epsilon_(o))`

=
`(4.60 * 10^(-12)C/m^(2))/(2 * 8.854 * 10^(-12)C^(2)/N m^(2))`

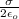
= 0.259 N/C

Now, force will be calculated as follows.

F = Eq

=
`0.259 N/C * 1.6 * 10^(-19) C`

=
`0.415 * 10^(-19) N`

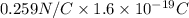
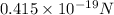
Now, work done will be as follows.

W = Fs

=
`0.415 * 10^(-19) N * 0.51 m`

=
`2.12 * 10^(-20) J`

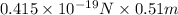
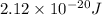
Thus, we can conclude that work done on the electron by the electric field of the sheet is
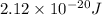`2.12 * 10^(-20) J`.