Question

The nth term of a sequence is 2n2 + 1 The nth term of a different sequence is 65 - 2n2. Show that there is only 1 number that is in both of these sequences

Answer 1

The only common term is 33.

Explanation:

We are given the following in the question:

Sequence 1:

`n^(th)\text{ term: } 2n^2 + 1`

Sequence 2:

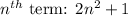
`n^(th)\text{ term: } 65 - 2n^2`

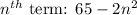
Equating the two terms, we get,

`2n^2 + 1 = 65 - 2n^2\\4n^2 = 64\\\\n^2 = (64)/(4)\\\\n^2 = 16\\n = \pm 4`

Since, n cannot take a negative value, we get n = 4.

Thus, there is only 1 common term both the series have for n = 4.

Common term:

`2(4)^2+ 1 - 65-2(4)^2 = 33`

Thus, the only common term is 33.