Question

A student was trying to determine the mole percent of A in a mixture of A and B using refractive index. If their mixture has a refractive index of 1.5248 and pure A and pure B each had refractive indices of 1.7058 and 1.3658, respectively, what was the mole percent of A in their mixture. Type your numerical answer rounded to the 3rd decimal place (i.e. 45.982 or 9.550, etc) without a percent sign.

Answer 1

Step-by-step explanation:

Formula to calculate refractive index of n is as follows.

n =
`X_(A) * n_(A) + X_(B) * n_(B)`

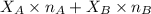
where,
`X_(A)` = mole fraction of A

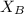`X_(B)` = mole fraction of B

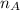`n_(A)` = refractive index of A

`n_(B)` = refractive index of B

Hence, putting the given values into the above formula as follows.

n =
`X_(A) * n_(A) + X_(B) * n_(B)`

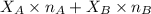
1.5248 =
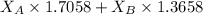`X_(A) * 1.7058 + X_(B) * 1.3658` ........ (1)

Also, it is known that
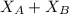`X_(A) + X_(B)` = 1

and,
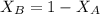`X_(B) = 1 - X_(A)` ......... (2)

Now, put equation (2) in equation (1) as follows.

1.5248 =
`X_(A) * 1.7058 + 1 - X_(A) * 1.3658`

1.5248 =
`X_(A) * 1.7058 + 1.3658 - 1.3658X_(A)`

`X_(A)` = 0.467

And, the value of
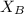`X_(B)` is calculated as follows.

`X_(B) = 1 - X_(A)`

=
`1 - 0.467`

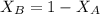
= 0.533

Hence, mole percentage of A will be calculated as follows.

Mole % of A =
`(n_(A))/(n_(A) + n_(B))`

=
`(0.467)/(0.467 + 0.533) * 100`

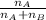
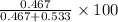
= 46.7%

Thus, we can conclude that the mole percent of A in their mixture is 46.7%.