Answer:
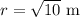
Explanation:
We have been given that when a cylindrical tank is filled with water at a rate of 22 cubic meters per hour, the level of water in the tank rises at a rate of 0.7 meters per hour. We are asked to find the approximate radius of tank in meters.
We will use volume of cylinder formula to solve our given problem as:
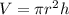 , where,
, where,
r = Radius,
h = Height of cylinder.
Since the level of water in the tank rises at a rate of 0.7 meters per hour, so height of cylinder would be
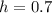 meters at
meters at
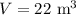 .
.
Upon substituting these values in above formula, we will get:
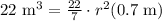
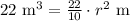



Now, we will take positive square root of both sides as radius cannot be negative.

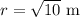
Therefore, radius of tank would be approximately square root of 10 m.