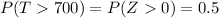Question

Let X and Y be the number of hours that a randomly selected person watches Game of Thrones and Star Wars, respectively, during a three-month period. The following information is known about X and Y:E(X) = 50, E(Y) = 20, Var(X) = 50, Var(Y) = 30, Cov(X, Y) = 10. One hundred people are randomly selected and observed for these three months. Let T be the total number of hours that these one hundred people watch Game of Thrones or Star Wars during this three-month period. Approximate the value of P(T < 700). Hint: Let Ti be the total number of hours person i watches Game of Thrones or Star Wars during this three-month period.

Answer 1

`E(T) = E(X+Y) = E(X) + E(Y) = 50 + 20 = 70`

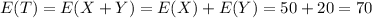
And the variance can be founded like this:

`Var(T) = Var(X+Y) = Var(X) + Var(Y) + 2 Cov (X,Y) = 50+30 + 2*10 =100`

`Sd(T) = √(100)=10`

`z = (T/n -\bar T)/((\sigma)/(√(n)))`

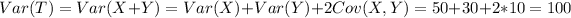
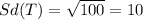
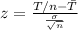
And if we use this formula we got:

`z= (700/100 -70)/((10)/(√(100)))= 0`

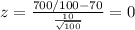
So then we have this:

`P(T>700) = P(Z >0) = 0.5`

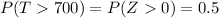
Explanation:

For this case we have the following data given:

`E(X) = 50, E(Y)= 20 , Var(X) = 50, Var(Y) = 30, Cov (X,Y) = 10`

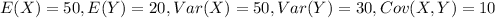
We define the random variable T as the total number of hours that the people watch Games of Thrones or star Wars. So then we can define
`T = X+Y`

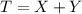
We can find the expected value of T like this:

`E(T) = E(X+Y) = E(X) + E(Y) = 50 + 20 = 70`

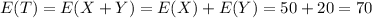
And the variance can be founded like this:

`Var(T) = Var(X+Y) = Var(X) + Var(Y) + 2 Cov (X,Y) = 50+30 + 2*10 =100`

`Sd(T) = √(100)=10`

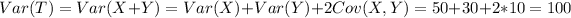
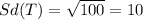
We know that the sampel mena is defined as:

`\bar T = (\sum_(i=1)^n T_i)/(n)= (T)/(n)`

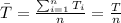
And for this case since the sampel large is enough n>30, we have that the distribution for T can be approximated with the normal distribution using the central limit theorem:

`\bar T \sim N (T/n , (\sigma)/(√(n)))`

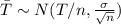
We want to calculate the following probability:

`P(T>700)`

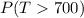
We can use the z score formula given by:

`z = (T/n -\bar T)/((\sigma)/(√(n)))`

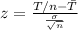
And if we use this formula we got:

`z= (700/100 -70)/((10)/(√(100)))= 0`

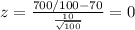
So then we have this:

`P(T>700) = P(Z >0) = 0.5`