Incomplete question.The complete question is here
To throw the discus, the thrower holds it with a fully outstretched arm. Starting from rest, he begins to turn with a constant angular acceleration, releasing the discus after making one complete revolution. The diameter of the circle in which the discus moves is about 1.7 m.If the thrower takes 1.0 s to complete one revolution, starting from rest, what will be the speed of the discus at release?
Answer:
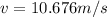
Step-by-step explanation:
Radius r=1.7m/2 =0.85 m
The angular displacement in time t is:
θ=1/2αt²
where α is angular acceleration
Given
θ=2π
t=1.0s
So
α=2θ/t²
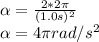
Angular speed after 1.0s is:
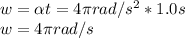
Speed of discus is given by: