Answer:

So we have at least 88.89% of the noise level values within 3 deviation from the mean.
Explanation:
For this case let define the random variable X as the noise level, we know the following properties for X:
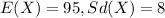
And for this case we don't know the distribution for the random variable X.
But we can use the Chebysev theorem who states that the minimum percentage of the data that lies within k standard deviations from the mean is given by:

So for this case we have that k = 3 and if we use this theorem we have:
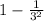
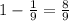
And we can convert this into % and we got:

So we have at least 88.89% of the noise level values within 3 deviation from the mean.