Question

A uniform steel rod of cross-sectional area A is attached to rigid supports and is unstressed at a temperature of 458F. The steel is assumed to be elastoplastic with sY 5 36 ksi and E 5 29 3 106 psi. Knowing that a 5 6.5 3 1026 /8F, determine the stress in the bar (a) when the temperature is raised to 3208F, (b) after the temperature has returned to 458F.

Answer 1

(a). The stress is
`-51.83*10^(3)\ psi`

(b). The residual stress is 15.83 ksi

Step-by-step explanation:

Given that,

Initial temperature = 45°F

Raised temperature = 320°F

`\sigma_(y)=36\ ksi`

`E=29*10^(6)\ psi`

`\alpha=6.5*10^(-6)\ /^(\circ)F`

We need to calculate the actual change in temperature

`\Delta T_(a)=320-45=275^(\circ)F`

We need to calculate the stress

Using formula of stress

`\sigma'=(P)/(A)`

`\sigma'=-(AE\alpha\Delta T)/(A)`

`\sigma'=-E\alpha\Delta T`

Put the value into the formula

`\sigma'=-29*10^(6)*6.5*10^(-6)*275`

`\sigma'=-51.83*10^(3)\ psi`

(b). We need to calculate the residual stress

Using formula of stress

`\sigma_(r)=-\sigma_(y)-\sigma'`

Put the value into the formula

`\sigma_(r)=-36+51.83*10^(3)`

`\sigma_(r)=15.83\ ksi`

Hence, (a). The stress is
`-51.83*10^(3)\ psi`

(b). The residual stress is 15.83 ksi

Answer 2

Step-by-step explanation:

As the given rod is attached to rigid supports as a result, the deformation occurring due to the change in temperature will cause stress in the rod.

Let us assume that P is the compressive force in the rod due to change in temperature.

So,
`\Delta T = (\sigma_(y))/(E_(a))`

=
`(36 * 10^(3))/((29 * 10^(6) * 6.5 * 10^(-6)))`

=
`190.98^(o)F`

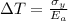
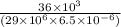
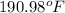
Now, we will calculate the actual change in temperature as follows.

`\Delta T = 320 - 45 = 275^(o)F`

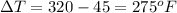
This means that the actual change in temperature is more than required for yielding.

(a) Formula to calculate yielding stress is as follows.

`\sigma' = (P')/(A)`

`\sigma' = -(AE \alpha \Delta T)/(A)`

=
`-E \alpha \Delta T`

=
`-29 * 10^(6) * 6.5 * 10^(-6) * 275`

=
`-51.8375 * 10^(3) psi`

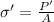
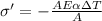
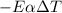
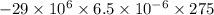
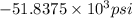
Hence, stress in the bar when temperature is raised to
`320^(o)F` is
`-51.8375 * 10^(3) psi`.

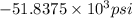(b) Now, we will calculate the residual stress as follows.

`\sigma_(r) = -\sigma_(y) - \sigma'`

`\sigma_(r) = -36 + 51.837 ksi`

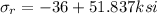
= 15.837 ksi

Therefore, stress in the bar when the temperature has returned to
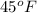`45^(o)F` is 15.837 ksi.