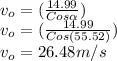Question

9. A football punter attempts to kick the football so that it lands on the ground 67.0 m from where it is kicked and stays in the air for 4.50 s. At what angle and with what initial speed should the ball be kicked? Assume that the ball leaves the punker’s foot at a height of 1.23 m.

Answer 1

Angle is 55.52°

and Initial Speed is v=26.48 m/s

Step-by-step explanation:

Given data

`x_(o)=0m\\ y_(o)=1.23m\\a_(oy)=a_(1y)=g=-9.8m/s^(2) \\x_(1)=67.0m\\y_(1)=0m\\t_(o)=0\\a_(ox)=m/s^(2) \\t_(1)=4.50s`

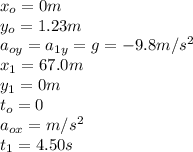
Applying the kinematics equations for motion with uniform acceleration in x and y direction

So

`x_(1)=x_(o)+v_(ox)t_(1)=67.0m\\0+4.50v_(o)Cos\alpha =67.0m\\v_(o)Cos\alpha =14.99\\v_(o)=14.99/Cos\alpha.....(1) \\and\\y_(1)=y_(o)+v_(oy)t_(1)+(1/2)a_(oy)t_(1)^(2) =0m\\ 1+4.50v_(o)Sin\alpha+(-9.8/2)(4.5)^(2)=0\\ v_(o)Sin\alpha=21.828.....(2)`

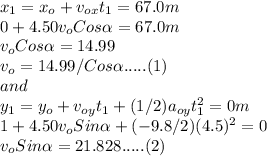
Put the value of v₀ from equation (1) to equation (2)

So

`(14.99)/(Cos\alpha )(Sin\alpha ) =21.828\\as\\tan\alpha =Sin\alpha /Cos\alpha \\So\\14.99tan\alpha =21.828\\tan\alpha =21.828/14.99\\\alpha =tan^(-1)(21.828/14.99) \\\alpha =55.52^(o)`

Put that angle in equation (1) or equation (2) to find the initial velocity

So from equation (1)

`v_(o)=((14.99)/(Cos\alpha ) ) \\v_(o)=((14.99)/(Cos(55.52) ) ) \\v_(o)=26.48m/s`